https://school.programmers.co.kr/learn/courses/30/lessons/138475
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
내가 등장한 문제라 재밌게 풀었다
문제 설명
영우는 천하제일 암산대회를 앞두고 있습니다. 암산보다는 암기에 일가견이 있는 영우는 구구단을 확장하여 억억단을 만들고 외워버리기로 하였습니다.
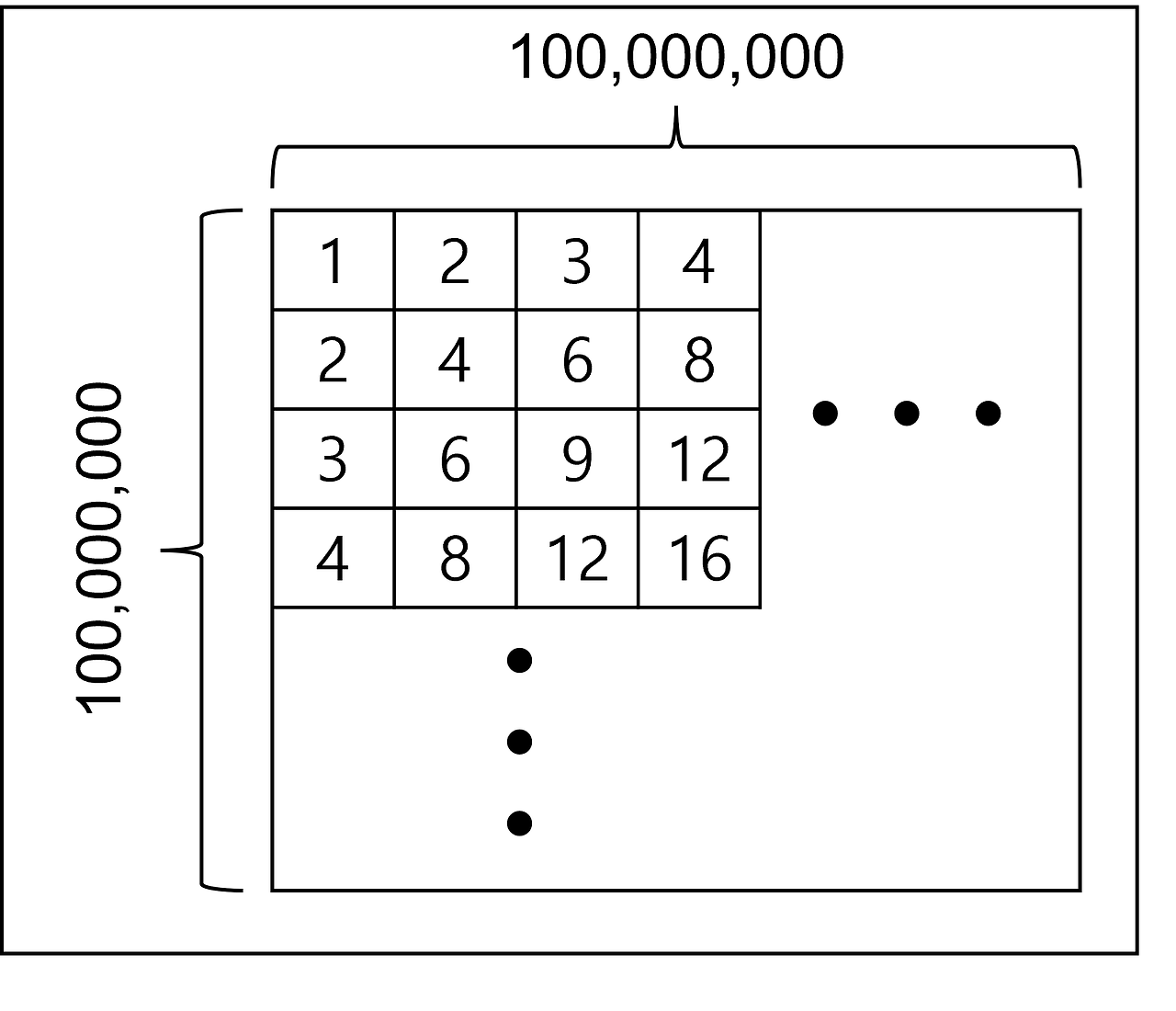
억억단은 1억 x 1억 크기의 행렬입니다. 억억단을 외우던 영우는 친구 수연에게 퀴즈를 내달라고 부탁하였습니다.
수연은 평범하게 문제를 내봐야 영우가 너무 쉽게 맞히기 때문에 좀 어렵게 퀴즈를 내보려고 합니다. 적당한 수 e를 먼저 정하여 알려주고 e 이하의 임의의 수 s를 여러 개 얘기합니다. 영우는 각 s에 대해서 s보다 크거나 같고 e 보다 작거나 같은 수 중에서 억억단에서 가장 많이 등장한 수를 답해야 합니다. 만약 가장 많이 등장한 수가 여러 개라면 그 중 가장 작은 수를 답해야 합니다.
수연은 영우가 정답을 말하는지 확인하기 위해 당신에게 프로그램 제작을 의뢰하였습니다. e와 s의 목록 starts가 매개변수로 주어질 때 각 퀴즈의 답 목록을 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ e ≤ 5,000,000
- 1 ≤ starts의 길이 ≤ min {e,100,000}
- 1 ≤ starts의 원소 ≤ e
- starts에는 중복되는 원소가 존재하지 않습니다.
입출력 예
| e | starts | result |
| 8 | [1,3,7] | [6,6,8] |
입출력 예 설명
억억단에서 1 ~ 8이 등장하는 횟수는 다음과 같습니다.
1번 등장 : 1
2번 등장 : 2, 3, 5, 7
3번 등장 : 4
4번 등장 : 6, 8
[1, 8] 범위에서는 6과 8이 각각 4번씩 등장하여 가장 많은데 6이 더 작은 수이므로 6이 정답입니다.
[3, 8] 범위에서도 위와 같으므로 6이 정답입니다.
[7, 8] 범위에서는 7은 2번, 8은 4번 등장하므로 8이 정답입니다.
문제 솔루션
1. 1 ⪯ e ⪯ 500만
2. starts 의 길이 1 ⪯ starts.length ⪯ 10만
3. 1 ⪯ s ⪯ e
해당 문제는 starts 의 각 s 에 대해서 s ~ e 까지의 약수의 개수를 모두 구하고 그 중 가장 등장횟수가 많고, 작은 값이 무엇인지 구하는 것이다.
핵심은 다음과 같다.
조건을 "가장 등장횟수가 많고, 작은 값" 라고 하자.
1. 1 ~ e 까지의 모든 수에 대해서 등장 횟수를 어떻게 구할 것인가?
2. 구해진 등장 횟수를 이용하여 어떻게 s ~ e 구간의 조건 을 만족하는 값을 구할 것인가?
핵심 알고리즘 : 메모리제이션
1. 등장 횟수를 어떻게 구할 것인가에 대해서는 이중 반복문을 이용하여 counts 배열을 완성할 수 있다.
2. 완성된 counts 를 활용하여 dp 를 완성하는데, dp[i][0] 은 i ~ e 까지 중 조건을 만족하는 가장 작은 값이며, dp[i][1] 은 dp[i][0] 이 등장한 횟수를 저장한다.
- dp[i] 는 counts[i] 와 dp[i + 1] 을 이용하여 계산하면 된다.
시간복잡도
1. 등장 횟수를 구하기
public void getAppearanceCounts(int e, int[] counts) {
for (int i = 1; i <= e; i++) {
for (int j = 1; j <= e/i; j++) {
counts[i * j] += 1;
}
}
}
int[] counts = new int[e + 1];
getAppearanceCounts(e, counts);
i 가 1 부터 e 까지 e/i 씩 반복한다. 따라서 이를 수학적으로 적으면
조화급수의 형태를 띈다. 각 [ ] 그룹의 합이 0.5 가 되도록 설정하게 만든다면, 그 개수를 log₂ e 개 존재한다. 따라서, O(e * log e) 이다.

2. s 와 e 사이의 조건을 만족하는 값 구하기
starts 의 길이가 최대 10만이므로, 효율적으로 찾아낼 수 있어야 한다. 따라서, s 가 바뀌는 값이므로, dp 를 거꾸로 채우면 된다. 따라서 시간복잡도는 O(e) 이다.
전체 시간 복잡도 O(e · log e) 이다.
트러블 슈팅
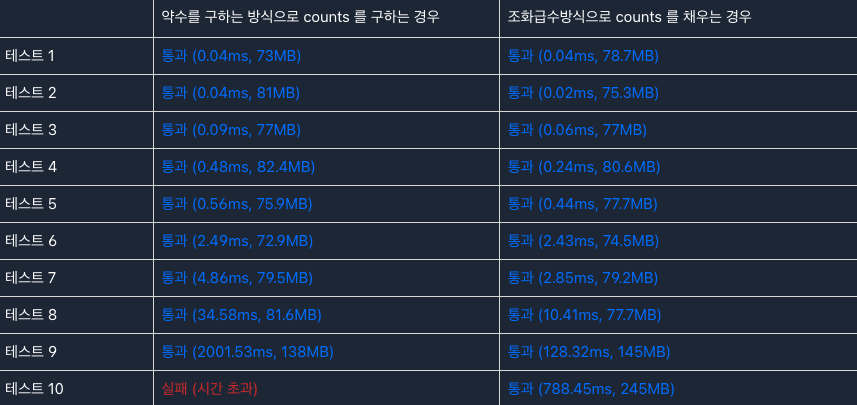
등장 횟수를 구하는 방법은 각 숫자의 약수의 개수를 구하는 방법으로도 구할 수 있다.
이 경우에는 e 에 대해서, √e 만큼 동작하기에 O(e ·√e) 이 됩니다.
따라서, e 가 최대 500만 이므로, 약 111억의 연산이 일어난다.
1 ~ e 까지의 모든 값에 대해서 찾아야 하므로, 해당 방법은 문제가 될 수 있다.
public int getAppearanceCount(int num) {
int count = 0;
int sqrt = (int) Math.sqrt(num);
for (int i = 1; i <= sqrt; i++) {
if (num % i == 0) {
count += num / i != i ? 2 : 1;
}
}
return count;
}
int[] counts = new int[e + 1];
for (int i = 1; i <= e; i++) {
counts[i] = getAppearanceCount(i);
}
전체 코드
import java.util.*;
class Solution {
private static final int NUM = 0;
private static final int COUNT = 1;
public int[] solution(int e, int[] starts) {
int[] answers = new int[starts.length];
int[] counts = new int[e + 1];
int[][] dp = new int[e + 1][2];
// dp[i][0] : i ~ e 사이의 가장 많이 등장한 가장 작은 수
// dp[i][1] : dp[i][0] 의 등장 횟수
getAppearanceCounts(e, counts);
dp[e][NUM] = e;
dp[e][COUNT] = counts[e];
for (int i = e - 1; i >= 1; i--) {
if (counts[i] >= dp[i + 1][COUNT]) {
dp[i][NUM] = i;
dp[i][COUNT] = counts[i];
} else {
dp[i][NUM] = dp[i + 1][NUM];
dp[i][COUNT] = dp[i + 1][COUNT];
}
}
for (int i = 0; i < starts.length; i++) {
int s = starts[i];
answers[i] = dp[s][NUM];
}
return answers;
}
public void getAppearanceCounts(int e, int[] counts) {
for (int i = 1; i <= e; i++) {
for (int j = 1; j <= e/i; j++) {
counts[i * j] += 1;
}
}
}
}https://school.programmers.co.kr/learn/courses/30/lessons/138475
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
내가 등장한 문제라 재밌게 풀었다
문제 설명
영우는 천하제일 암산대회를 앞두고 있습니다. 암산보다는 암기에 일가견이 있는 영우는 구구단을 확장하여 억억단을 만들고 외워버리기로 하였습니다.

억억단은 1억 x 1억 크기의 행렬입니다. 억억단을 외우던 영우는 친구 수연에게 퀴즈를 내달라고 부탁하였습니다.
수연은 평범하게 문제를 내봐야 영우가 너무 쉽게 맞히기 때문에 좀 어렵게 퀴즈를 내보려고 합니다. 적당한 수 e를 먼저 정하여 알려주고 e 이하의 임의의 수 s를 여러 개 얘기합니다. 영우는 각 s에 대해서 s보다 크거나 같고 e 보다 작거나 같은 수 중에서 억억단에서 가장 많이 등장한 수를 답해야 합니다. 만약 가장 많이 등장한 수가 여러 개라면 그 중 가장 작은 수를 답해야 합니다.
수연은 영우가 정답을 말하는지 확인하기 위해 당신에게 프로그램 제작을 의뢰하였습니다. e와 s의 목록 starts가 매개변수로 주어질 때 각 퀴즈의 답 목록을 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ e ≤ 5,000,000
- 1 ≤ starts의 길이 ≤ min {e,100,000}
- 1 ≤ starts의 원소 ≤ e
- starts에는 중복되는 원소가 존재하지 않습니다.
입출력 예
| e | starts | result |
| 8 | [1,3,7] | [6,6,8] |
입출력 예 설명
억억단에서 1 ~ 8이 등장하는 횟수는 다음과 같습니다.
1번 등장 : 1
2번 등장 : 2, 3, 5, 7
3번 등장 : 4
4번 등장 : 6, 8
[1, 8] 범위에서는 6과 8이 각각 4번씩 등장하여 가장 많은데 6이 더 작은 수이므로 6이 정답입니다.
[3, 8] 범위에서도 위와 같으므로 6이 정답입니다.
[7, 8] 범위에서는 7은 2번, 8은 4번 등장하므로 8이 정답입니다.
문제 솔루션
1. 1 ⪯ e ⪯ 500만
2. starts 의 길이 1 ⪯ starts.length ⪯ 10만
3. 1 ⪯ s ⪯ e
해당 문제는 starts 의 각 s 에 대해서 s ~ e 까지의 약수의 개수를 모두 구하고 그 중 가장 등장횟수가 많고, 작은 값이 무엇인지 구하는 것이다.
핵심은 다음과 같다.
조건을 "가장 등장횟수가 많고, 작은 값" 라고 하자.
1. 1 ~ e 까지의 모든 수에 대해서 등장 횟수를 어떻게 구할 것인가?
2. 구해진 등장 횟수를 이용하여 어떻게 s ~ e 구간의 조건 을 만족하는 값을 구할 것인가?
핵심 알고리즘 : 메모리제이션
1. 등장 횟수를 어떻게 구할 것인가에 대해서는 이중 반복문을 이용하여 counts 배열을 완성할 수 있다.
2. 완성된 counts 를 활용하여 dp 를 완성하는데, dp[i][0] 은 i ~ e 까지 중 조건을 만족하는 가장 작은 값이며, dp[i][1] 은 dp[i][0] 이 등장한 횟수를 저장한다.
- dp[i] 는 counts[i] 와 dp[i + 1] 을 이용하여 계산하면 된다.
시간복잡도
1. 등장 횟수를 구하기
public void getAppearanceCounts(int e, int[] counts) {
for (int i = 1; i <= e; i++) {
for (int j = 1; j <= e/i; j++) {
counts[i * j] += 1;
}
}
}
int[] counts = new int[e + 1];
getAppearanceCounts(e, counts);
i 가 1 부터 e 까지 e/i 씩 반복한다. 따라서 이를 수학적으로 적으면
조화급수의 형태를 띈다. 각 [ ] 그룹의 합이 0.5 가 되도록 설정하게 만든다면, 그 개수를 log₂ e 개 존재한다. 따라서, O(e * log e) 이다.

2. s 와 e 사이의 조건을 만족하는 값 구하기
starts 의 길이가 최대 10만이므로, 효율적으로 찾아낼 수 있어야 한다. 따라서, s 가 바뀌는 값이므로, dp 를 거꾸로 채우면 된다. 따라서 시간복잡도는 O(e) 이다.
전체 시간 복잡도 O(e · log e) 이다.
트러블 슈팅
등장 횟수를 구하는 방법은 각 숫자의 약수의 개수를 구하는 방법으로도 구할 수 있다.
이 경우에는 e 에 대해서, √e 만큼 동작하기에 O(e ·√e) 이 됩니다.
따라서, e 가 최대 500만 이므로, 약 111억의 연산이 일어난다.
1 ~ e 까지의 모든 값에 대해서 찾아야 하므로, 해당 방법은 문제가 될 수 있다.
public int getAppearanceCount(int num) {
int count = 0;
int sqrt = (int) Math.sqrt(num);
for (int i = 1; i <= sqrt; i++) {
if (num % i == 0) {
count += num / i != i ? 2 : 1;
}
}
return count;
}
int[] counts = new int[e + 1];
for (int i = 1; i <= e; i++) {
counts[i] = getAppearanceCount(i);
}
전체 코드
import java.util.*;
class Solution {
private static final int NUM = 0;
private static final int COUNT = 1;
public int[] solution(int e, int[] starts) {
int[] answers = new int[starts.length];
int[] counts = new int[e + 1];
int[][] dp = new int[e + 1][2];
// dp[i][0] : i ~ e 사이의 가장 많이 등장한 가장 작은 수
// dp[i][1] : dp[i][0] 의 등장 횟수
getAppearanceCounts(e, counts);
dp[e][NUM] = e;
dp[e][COUNT] = counts[e];
for (int i = e - 1; i >= 1; i--) {
if (counts[i] >= dp[i + 1][COUNT]) {
dp[i][NUM] = i;
dp[i][COUNT] = counts[i];
} else {
dp[i][NUM] = dp[i + 1][NUM];
dp[i][COUNT] = dp[i + 1][COUNT];
}
}
for (int i = 0; i < starts.length; i++) {
int s = starts[i];
answers[i] = dp[s][NUM];
}
return answers;
}
public void getAppearanceCounts(int e, int[] counts) {
for (int i = 1; i <= e; i++) {
for (int j = 1; j <= e/i; j++) {
counts[i * j] += 1;
}
}
}
}